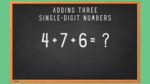Mathematics – United States – Common Core State Standards
2.OA – Operations & Algebraic Thinking
Mathematics
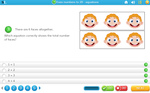
2.OA.1 – Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem. (See Glossary, Table 1. http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ )
-
14 learning outcomes – click to view
Samples: Adding multiples of 10. Adding two digit numbers (split strategy). Adding on (numbers under 10).
-
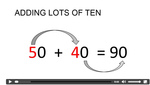
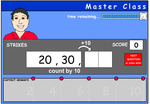
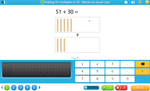
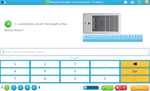
Adding multiples of 10
- Activities: 3 course, 4 extra
-
-
- Adding multiples of 10
- Tutorial
-
-
-
- Adding multiples of 10.
- Practice
-
-
-
- Adding multiples of 10
- Tutorial
-
Extra activities
-
-
- Adding multiples of 10
- Printable
-
-
-
- Adding multiples of 10
- Tutorial
-
-
-

- Addition problem solving
- Assessment
-
-
-

- Adding lots of 10
- Practice
-
-
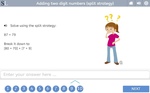
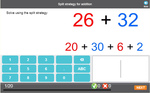
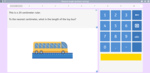
Adding two-digit numbers using the split strategy
- Activities: 5 course, 2 extra
-
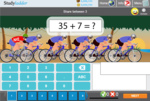
Adding single-digit numbers to two-digit numbers
- Activities: 3 course, 14 extra
-
-
- Adding on (numbers under 10)
- Tutorial
-
-
-
- Adding on (numbers under 10)
- Practice
-
-
-
- Adding on (numbers under 10)
- Challenge
-
Extra activities
-
-
- Adding on (numbers under 10)
- Printable
-
-
-
- Adding on (numbers under 10)
- Printable
-
-
-
- Add on numbers under 10
- Tutorial
-
-
-

- Add on numbers less than 10
- Assessment
-
-
-

- Add lots of 10 - Jump Strategy
- Practice
-
-
-

- Adding lots of 10 to numbers less than 200
- Assessment
-
-
-

- Adding lots of 10 to numbers less than 1,000
- Assessment
-
-
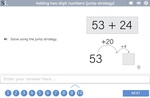
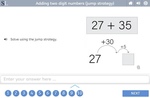
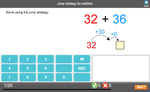
Adding two-digit numbers using the jump strategy
- Activities: 6 course, 5 extra
Extra activities
-
-
- Jump Strategy/Method Explained
- Tutorial
-
-
-
- Jump Strategy/Method
- Tutorial
-
-
-

- Addition of two digit numbers
- Challenge
-
-
-

- Addition of Two Digit Numbers
- Assessment
-
-
Adding two-digit numbers using the written strategy
- Activities: 5 course, 8 extra
Extra activities
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Tutorial
-
-
Adding two digit numbers - problem solving
- Activities: 6 course, 12 extra
Extra activities
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Addition of two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-

- Problem solving using addition
- Assessment
-
-
-
- Subtraction - two digit numbers
- Printable
-
-
-

- Addition of two digit numbers
- Assessment
-
-
-

- Addition using the Jump Strategy/Method
- Challenge
-
-
Challenge Puzzle - Addition Pyramid
- Activities: 1 course, 0 extra
-
-
- Challenge Puzzle - Addition Pyramid
- Practice
-
-
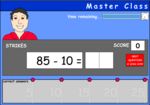
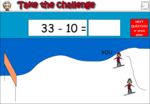
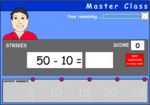
Subtracting 10
- Activities: 7 course, 12 extra
-
-
- Subtracting 10
- Tutorial
-
-
-
- Subtract 10
- Practice
-
-
-
- Subtracting 10 (problem solving)
- Practice
-
-
-
- Subtracting 10
- Printable
-
-
-
- Subtracting 10
- Tutorial
-
-
-
- Subtracting 10
- Challenge
-
-
-
- Subtracting 10
- Practice
-
Extra activities
-
-
- Subtracting 10
- Printable
-
-
-
- Subtracting 10 (problem solving)
- Printable
-
-
-
- Subtracting 10 (problem solving)
- Printable
-
-
-
- Subtract 10 from numbers under 100
- Printable
-
-
-
- Subtract 10 from larger numbers
- Printable
-
-
-
- Subtract 10 from numbers
- Printable
-
-
-

- Subtract 10 from larger numbers
- Assessment
-
-
-

- Subtract 10 from larger numbers
- Challenge
-
-
-

- Subtract 10 from numbers
- Assessment
-
-
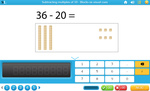
Subtracting multiples of 10
- Activities: 4 course, 7 extra
-
-
- Subtracting multiples of 10
- Tutorial
-
-
-
- Subtracting multiples of 10
- Practice
-
-
-
- Subtracting multiples of 10
- Tutorial
-
Extra activities
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtract Multiples Of 10
- Tutorial
-
-
Subtracting from 100
- Activities: 6 course, 7 extra
-
-
- Subtracting from 100
- Tutorial
-
-
-
- Subtracting from 100
- Practice
-
-
-
- Subtracting from 100
- Challenge
-
-
-
- Subtracting from 100
- Tutorial
-
-
-
- Subtracting from 100
- Tutorial
-
Extra activities
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtract from 100
- Printable
-
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtract from 100 - Written Strategy
- Tutorial
-
-
-

- Subtract from 100
- Practice
-
-
-

- Subtract from 100
- Assessment
-
-
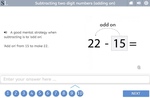
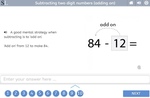
Subtracting two digit numbers (adding on)
- Activities: 5 course, 0 extra
-
-
- Add on to subtract
- Practice
-
-
-
- Add on to subtract
- Practice
-
-
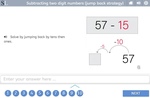
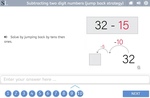
Subtracting two digit numbers (jump back strategy)
- Activities: 5 course, 16 extra
-
-
- Subtracting (jumping back)
- Tutorial
-
Extra activities
-
-

- Subtract 20 from numbers under 100
- Challenge
-
-
-

- Subtract 20 from numbers under 100
- Assessment
-
-
-

- Subtract 30 from numbers under 100
- Challenge
-
-
-

- Subtract 30 from numbers under 100
- Assessment
-
-
-

- Subtract 40 from numbers under 100
- Assessment
-
-
-

- Subtract 40 from numbers under 100
- Challenge
-
-
-

- Subtract 50 from numbers under 100
- Challenge
-
-
-

- Subtract 50 from numbers under 100
- Assessment
-
-
Subtracting two digit numbers (written strategy)
- Activities: 6 course, 10 extra
Extra activities
-
-
- Subtraction of two digit numbers
- Printable
-
-
-

- Subtraction - two digit numbers
- Practice
-
-
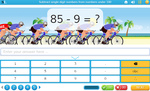
Subtracting two digit numbers
- Activities: 6 course, 22 extra
-
-
- Subtracting two digit numbers
- Practice
-
Extra activities
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtract numbers less than 20
- Printable
-
-
-
- Drill - Subtract numbers up to 100
- Printable
-
-
-

- Problem solving using subtraction
- Assessment
-
-
-

- Subtraction
- Assessment
-
-
-

- Subtraction - two digit numbers
- Challenge
-
-
-

- Subtraction of two digit numbers
- Challenge
-
-
-

- Subtraction of two digit numbers
- Assessment
-
-
-
14 learning outcomes – click to view
Mathematics
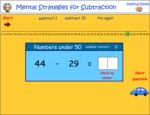
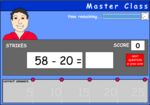
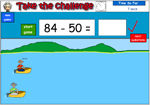
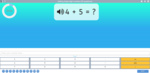
2.OA.2 – Fluently add and subtract within 20 using mental strategies. (See standard 1.OA.6 for a list of mental strategies.) By end of Grade 2, know from memory all sums of two one-digit numbers.
-
4 learning outcomes – click to view
Samples: Adding single digit numbers. Single digit addition (missing number). Subtracting single digit numbers.
-
Adding single-digit numbers - number skills
- Activities: 7 course, 17 extra
-
-
- Adding single digit numbers
- Tutorial
-
-
-
- Adding single digit numbers
- Tutorial
-
-
-
- Adding single digit numbers
- Tutorial
-
-
-
- Adding single digit numbers
- Practice
-
-
-
- Adding single digit numbers
- Challenge
-
-
-
- Add numbers less than 5
- Tutorial
-
Extra activities
-
-
- Adding single digit numbers
- Printable
-
-
-
- Add doubles - single digit numbers
- Printable
-
-
-
- Adding single digit numbers
- Printable
-
-
-
- Adding single digit numbers
- Printable
-
-
-
- Timed Challenge: Add numbers less than 5
- Challenge
-
-
-

- Add Single Digits Duck Game
- Practice
-
-
-
- Drill - Add numbers up to 10.
- Printable
-
-
-
- Drill - Doubles to 20
- Printable
-
-
-

- Drill - Doubles to 20 (Auto-Generated)
- Printable
-
-
-
- Add single digit numbers
- Printable
-
-
-

- Addition to 20 - with visual cues
- Practice
-
-
-

- Add numbers less than 5
- Assessment
-
-
-

- Add single digit numbers
- Assessment
-
-
-

- Combining to 20
- Practice
-
-
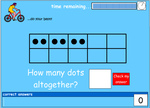
Single-digit addition (missing number)
- Activities: 5 course, 10 extra
-
-
- Single digit addition (missing number)
- Challenge
-
Extra activities
-
-
- Single digit addition (missing number)
- Printable
-
-
-
- Single digit addition (missing number)
- Printable
-
-
-
- Single digit addition (missing number)
- Printable
-
-
-
- Single digit addition (missing number)
- Printable
-
-
-
- Single digit addition (missing number)
- Printable
-
-
-
- Single digit addition (missing number)
- Printable
-
-
-

- Addition with a missing number
- Assessment
-
-
Subtracting single-digit numbers
- Activities: 4 course, 12 extra
-
-
- Subtracting single digit numbers
- Tutorial
-
-
-
- Subtracting single digit numbers
- Practice
-
-
-
- Subtracting single digit numbers
- Challenge
-
Extra activities
-
-
- Subtract single digit numbers
- Printable
-
-
-

- Subtraction problem solving
- Assessment
-
-
-
- Subtract single digit numbers
- Printable
-
-
-
- Drill - Subtraction under 10
- Printable
-
-
-
- Subtract single digit numbers
- Tutorial
-
-
-
- Subtract single digits
- Tutorial
-
-
-

- Subtract from 10
- Practice
-
-
-

- Subtract single digit numbers
- Assessment
-
-
-

- Subtract single digit numbers
- Challenge
-
-
-

- Subtract single digit numbers
- Practice
-
-
-

- Subtract numbers less than 20
- Assessment
-
-
-
4 learning outcomes – click to view
Mathematics
2.OA.3 – Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2s; write an equation to express an even number as a sum of two equal addends.
-
2 learning outcomes – click to view
Samples: Odd or Even amounts. Even numbers to 20 - equations.
-
2 learning outcomes – click to view
2.OA.4 – Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends.
-
6 learning outcomes – click to view
Samples: Groups of 2. Counting on number line (by 2's). Groups of 5. Counting on number line (by 5's).
-
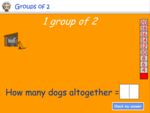
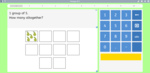
Groups of two
- Activities: 4 course, 7 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Counting in two's - rows
- Practice
-
-
-
- Counting in two's - groups
- Practice
-
-
-
- Groups of 2
- Tutorial
-
Extra activities
-
-
- Groups of 2
- Printable
-
-
-
- Groups of 2
- Printable
-
-
-

- Groups of 2
- Practice
-
-
-

- Groups of 2
- Challenge
-
-
-

- Groups of 2
- Assessment
-
-
-

- Multiply by adding lots of 2
- Practice
-
-
Counting on by two on a number line
- Activities: 7 course, 5 extra
-
-
- Counting on number line (by 2's)
- Tutorial
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by Two - Faster
- Tutorial
-
Extra activities
-
-
- Counting by 2
- Printable
-
-
-
- Counting by 2
- Tutorial
-
-
-

- Counting by 2
- Assessment
-
-
-

- Count on by 2 the next three numbers
- Practice
-
-
-

- Count by lots of 2
- Practice
-
-
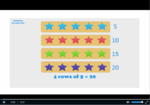
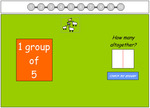
Groups of five
- Activities: 5 course, 14 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Practice
-
-
-
- Groups of 5
- Practice
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
Extra activities
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Identifying the amounts in a group
- Tutorial
-
-
-
- Groups and rows of 5
- Tutorial
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
-
-

- Groups of 5
- Challenge
-
-
-

- Groups of 5
- Practice
-
-
-

- Multiply by adding lots of 5
- Practice
-
-
-

- Groups of 5
- Assessment
-
-
-

- Rows of five
- Practice
-
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
-
- Counting on number line (by 5's)
- Tutorial
-
-
-
- Counting by 5
- Tutorial
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Tutorial
-
Extra activities
-
-
- Counting by 5
- Printable
-
-
-

- Counting by 5
- Assessment
-
-
-

- Count by lots of 5
- Practice
-
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
-
- Counting on number line (by 10's)
- Tutorial
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Tutorial
-
-
-
- Counting by 10
- Tutorial
-
Extra activities
-
-
- Counting by 10
- Printable
-
-
-
- Counting by 10
- Printable
-
-
-

- Numbers Problem Solving
- Assessment
-
-
-

- Count by lots of 10
- Practice
-
-
-

- Counting by 10
- Assessment
-
-
Arrays
- Activities: 4 course, 0 extra
-
-
- Arrays 2, 5, 10 (up to 5 rows)
- Practice
-
-
-
- Arrays 2, 5, 10 (up to 10 rows)
- Practice
-
-
-
- Arrays
- Practice
-
-
-
- Arrays 2, 5, 10 (up to 5 rows)
- Practice
-
-
-
6 learning outcomes – click to view
2.NBT – Number & Operations in Base Ten
Mathematics
2.NBT.1 – Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
2.NBT.1.a – 100 can be thought of as a bundle of ten tens — called a “hundred.”
-
3 learning outcomes – click to view
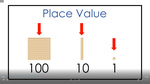
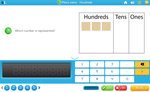
Samples: Place Values. Counting in tens and ones. Place Values teens: counting 15 sticks. Place Values. Place value 100.
-
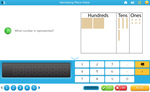
Numbers represented using MAB (up to 100)
- Activities: 3 course, 2 extra
-
-
- Place Values
- Tutorial
-
-
-
- Place Values
- Tutorial
-
Extra activities
-
-

- Identifying Place Value
- Practice
-
-
-

- Guessing game - Numbers to 100
- Practice
-
-
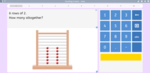
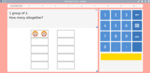
Counting in tens and ones
- Activities: 2 course, 2 extra
-
-
- Counting in tens and ones
- Practice
-
-
-
- Place value 100
- Practice
-
Extra activities
-
-
- Place value 100 concepts
- Printable
-
-
-
- Place value 100 - concepts Answer sheet
- Printable
-
-
-
3 learning outcomes – click to view
2.NBT.1.b – The numbers 100, 200, 300, 400, 500, 600, 700, 800, 900 refer to one, two, three, four, five, six, seven, eight, or nine hundreds (and 0 tens and 0 ones).
-
4 learning outcomes – click to view
Samples: Place value - hundreds, tens and ones. Place Values. Counting in tens and ones.
-
Place value - hundreds, tens and ones
- Activities: 4 course, 2 extra
-
Numbers represented using MAB (up to 100)
- Activities: 3 course, 2 extra
-
-
- Place Values
- Tutorial
-
-
-
- Place Values
- Tutorial
-
Extra activities
-
-

- Identifying Place Value
- Practice
-
-
-

- Guessing game - Numbers to 100
- Practice
-
-
Counting in tens and ones
- Activities: 2 course, 2 extra
-
-
- Counting in tens and ones
- Practice
-
-
-
- Place value 100
- Practice
-
Extra activities
-
-
- Place value 100 concepts
- Printable
-
-
-
- Place value 100 - concepts Answer sheet
- Printable
-
-
-
4 learning outcomes – click to view
2.NBT.2 – Count within 1000; skip-count by 5s, 10s, and 100s.
-
3 learning outcomes – click to view
Samples: Counting on number line (by 2's). Counting on number line (by 5's). Counting on number line (by 10's).
-
Counting by two
- Activities: 3 course, 10 extra
-
-
- Counting on number line (by 2's)
- Tutorial
-
-
-
- Skip Counting by 2's
- Practice
-
-
-
- Investigating number patterns
- Practice
-
Extra activities
-
-

- Count by 2
- Practice
-
-
-

- Count by 3
- Practice
-
-
-

- Count by 5
- Practice
-
-
-

- Continue a pattern by 3
- Practice
-
-
-

- Count by 2
- Practice
-
-
-

- Continue a pattern by 2 or 3
- Practice
-
-
-

- Continue a pattern by 5
- Practice
-
-
-

- Continue a pattern by 10
- Practice
-
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
-
- Counting on number line (by 5's)
- Tutorial
-
-
-
- Counting by 5
- Tutorial
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Tutorial
-
Extra activities
-
-
- Counting by 5
- Printable
-
-
-

- Counting by 5
- Assessment
-
-
-

- Count by lots of 5
- Practice
-
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
-
- Counting on number line (by 10's)
- Tutorial
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Tutorial
-
-
-
- Counting by 10
- Tutorial
-
Extra activities
-
-
- Counting by 10
- Printable
-
-
-
- Counting by 10
- Printable
-
-
-

- Numbers Problem Solving
- Assessment
-
-
-

- Count by lots of 10
- Practice
-
-
-

- Counting by 10
- Assessment
-
-
-
3 learning outcomes – click to view
2.NBT.3 – Read and write numbers to 1000 using base-ten numerals, number names, and expanded form.
-
3 learning outcomes – click to view
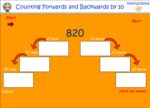
Samples: Place value. Writing numbers to 1000. Numbers written in expanded form. Counting forwards and backwards by 10.
-
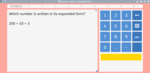
Numbers written in expanded form
- Activities: 1 course, 0 extra
-
-
- Numbers written in expanded form
- Practice
-
-
3 learning outcomes – click to view
2.NBT.4 – Compare two three-digit numbers based on meanings of the hundreds, tens, and ones digits, using >, =, and < symbols to record the results of comparisons.
-
1 learning outcomes – click to view
Samples: Comparing numbers to 1000 (< = >). Comparing numbers to 10,000 (<,=,>). Greater than or less than.
-
Comparing numbers to 1000 (< = >)
- Activities: 2 course, 1 extra
-
-
- Comparing numbers to 1000 (< = >)
- Practice
-
-
-
- Comparing numbers to 10,000 (<,=,>)
- Practice
-
Extra activities
-
-
- Greater than or less than
- Printable
-
-
-
1 learning outcomes – click to view
Mathematics
2.NBT.5 – Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
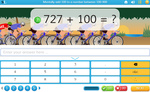
-
21 learning outcomes – click to view
Samples: Adding on single digit numbers using blocks. Adding two digit numbers using blocks. Adding multiples of 10.
-
Adding on single digit numbers using blocks
- Activities: 1 course, 0 extra
-
Adding two digit numbers using blocks
- Activities: 1 course, 0 extra
-
Adding multiples of 10
- Activities: 3 course, 4 extra
-
-
- Adding multiples of 10
- Tutorial
-
-
-
- Adding multiples of 10.
- Practice
-
-
-
- Adding multiples of 10
- Tutorial
-
Extra activities
-
-
- Adding multiples of 10
- Printable
-
-
-
- Adding multiples of 10
- Tutorial
-
-
-

- Addition problem solving
- Assessment
-
-
-

- Adding lots of 10
- Practice
-
-
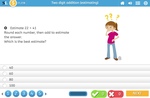
Adding two digit numbers by rounding then estimating
- Activities: 1 course, 2 extra
Extra activities
-
-
- Estimating
- Printable
-
-
-
- Estimating Answer sheet
- Printable
-
-
Adding two-digit numbers using the split strategy
- Activities: 5 course, 2 extra
-
Adding single-digit numbers to two-digit numbers
- Activities: 3 course, 14 extra
-
-
- Adding on (numbers under 10)
- Tutorial
-
-
-
- Adding on (numbers under 10)
- Practice
-
-
-
- Adding on (numbers under 10)
- Challenge
-
Extra activities
-
-
- Adding on (numbers under 10)
- Printable
-
-
-
- Adding on (numbers under 10)
- Printable
-
-
-
- Add on numbers under 10
- Tutorial
-
-
-

- Add on numbers less than 10
- Assessment
-
-
-

- Add lots of 10 - Jump Strategy
- Practice
-
-
-

- Adding lots of 10 to numbers less than 200
- Assessment
-
-
-

- Adding lots of 10 to numbers less than 1,000
- Assessment
-
-
Adding two-digit numbers using the jump strategy
- Activities: 6 course, 5 extra
Extra activities
-
-
- Jump Strategy/Method Explained
- Tutorial
-
-
-
- Jump Strategy/Method
- Tutorial
-
-
-

- Addition of two digit numbers
- Challenge
-
-
-

- Addition of Two Digit Numbers
- Assessment
-
-
Adding two-digit numbers using the written strategy
- Activities: 5 course, 8 extra
Extra activities
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Tutorial
-
-
Adding two digit numbers - problem solving
- Activities: 6 course, 12 extra
Extra activities
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-
- Addition of two digit numbers
- Printable
-
-
-
- Adding two digit numbers
- Printable
-
-
-

- Problem solving using addition
- Assessment
-
-
-
- Subtraction - two digit numbers
- Printable
-
-
-

- Addition of two digit numbers
- Assessment
-
-
-

- Addition using the Jump Strategy/Method
- Challenge
-
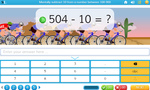
-
Subtracting 10
- Activities: 7 course, 12 extra
-
-
- Subtracting 10
- Tutorial
-
-
-
- Subtract 10
- Practice
-
-
-
- Subtracting 10 (problem solving)
- Practice
-
-
-
- Subtracting 10
- Printable
-
-
-
- Subtracting 10
- Tutorial
-
-
-
- Subtracting 10
- Challenge
-
-
-
- Subtracting 10
- Practice
-
Extra activities
-
-
- Subtracting 10
- Printable
-
-
-
- Subtracting 10 (problem solving)
- Printable
-
-
-
- Subtracting 10 (problem solving)
- Printable
-
-
-
- Subtract 10 from numbers under 100
- Printable
-
-
-
- Subtract 10 from larger numbers
- Printable
-
-
-
- Subtract 10 from numbers
- Printable
-
-
-

- Subtract 10 from larger numbers
- Assessment
-
-
-

- Subtract 10 from larger numbers
- Challenge
-
-
-

- Subtract 10 from numbers
- Assessment
-
-
Subtracting multiples of 10
- Activities: 4 course, 7 extra
-
-
- Subtracting multiples of 10
- Tutorial
-
-
-
- Subtracting multiples of 10
- Practice
-
-
-
- Subtracting multiples of 10
- Tutorial
-
Extra activities
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtracting multiples of 10
- Printable
-
-
-
- Subtract Multiples Of 10
- Tutorial
-
-
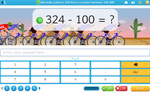
Subtracting from 100
- Activities: 6 course, 7 extra
-
-
- Subtracting from 100
- Tutorial
-
-
-
- Subtracting from 100
- Practice
-
-
-
- Subtracting from 100
- Challenge
-
-
-
- Subtracting from 100
- Tutorial
-
-
-
- Subtracting from 100
- Tutorial
-
Extra activities
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtract from 100
- Printable
-
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtracting from 100
- Printable
-
-
-
- Subtract from 100 - Written Strategy
- Tutorial
-
-
-

- Subtract from 100
- Practice
-
-
-

- Subtract from 100
- Assessment
-
-
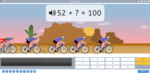
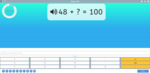
Adding to make 100
- Activities: 5 course, 3 extra
-
-
- Addition Make 100
- Tutorial
-
-
-
- Make 100
- Practice
-
-
-
- Make 100
- Practice
-
-
-
- Make 100
- Practice
-
-
-
- Addition - Make 100
- Practice
-
Extra activities
-
-
- Make 100
- Printable
-
-
-
- Make 100
- Printable
-
-
-
- Make 100 - Mental strategies
- Tutorial
-
-
Subtracting two digit numbers (adding on)
- Activities: 5 course, 0 extra
-
-
- Add on to subtract
- Practice
-
-
-
- Add on to subtract
- Practice
-
-
Subtracting two digit numbers (jump back strategy)
- Activities: 5 course, 16 extra
-
-
- Subtracting (jumping back)
- Tutorial
-
Extra activities
-
-

- Subtract 20 from numbers under 100
- Challenge
-
-
-

- Subtract 20 from numbers under 100
- Assessment
-
-
-

- Subtract 30 from numbers under 100
- Challenge
-
-
-

- Subtract 30 from numbers under 100
- Assessment
-
-
-

- Subtract 40 from numbers under 100
- Assessment
-
-
-

- Subtract 40 from numbers under 100
- Challenge
-
-
-

- Subtract 50 from numbers under 100
- Challenge
-
-
-

- Subtract 50 from numbers under 100
- Assessment
-
-
Subtracting two digit numbers (written strategy)
- Activities: 6 course, 10 extra
Extra activities
-
-
- Subtraction of two digit numbers
- Printable
-
-
-

- Subtraction - two digit numbers
- Practice
-
-
Subtracting two digit numbers
- Activities: 6 course, 22 extra
-
-
- Subtracting two digit numbers
- Practice
-
Extra activities
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtracting two digit numbers
- Printable
-
-
-
- Subtract numbers less than 20
- Printable
-
-
-
- Drill - Subtract numbers up to 100
- Printable
-
-
-

- Problem solving using subtraction
- Assessment
-
-
-

- Subtraction
- Assessment
-
-
-

- Subtraction - two digit numbers
- Challenge
-
-
-

- Subtraction of two digit numbers
- Challenge
-
-
-

- Subtraction of two digit numbers
- Assessment
-
-
Adding two digit numbers
- Activities: 2 course, 1 extra
-
-
- Adding two digit numbers
- Practice
-
-
-
- Adding two digit numbers
- Practice
-
Extra activities
-
-
- Adding two digit numbers
- Printable
-
-
Single Digit Subtraction Match
- Activities: 1 course, 0 extra
-
-
- Single Digit Subtraction Match
- Practice
-
-
-
21 learning outcomes – click to view
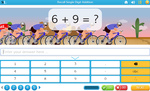
2.NBT.6 – Add up to four two-digit numbers using strategies based on place value and properties of operations.
-
12 learning outcomes – click to view
Samples: Adding three single digit numbers. Adding on 10 using blocks. Adding multiples of 10 using blocks.
-
Adding three numbers
- Activities: 7 course, 4 extra
-
-
- Adding three single digit numbers
- Tutorial
-
-
-
- Adding three single digit numbers
- Tutorial
-
-
-
- Adding three single digit numbers
- Tutorial
-
-
-
- Adding three single digit numbers
- Tutorial
-
-
-
- Adding three numbers (small numbers)
- Practice
-
-
-
- Add three sets of numbers
- Practice
-
Extra activities
-
-
- Adding three numbers (small numbers)
- Printable
-
-
-
- Adding three numbers
- Printable
-
-
-
- Add three single digit numbers
- Printable
-
-
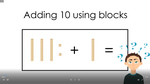
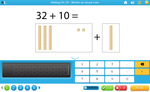
Adding on 10 using blocks
- Activities: 2 course, 0 extra
-
-
- Adding on 10 using blocks
- Tutorial
-
-
-
- Adding on 10 using blocks
- Practice
-
-
Adding multiples of 10 using blocks
- Activities: 2 course, 0 extra
-
-
- Adding multiples of 10 using blocks
- Tutorial
-
-
-
- Adding multiples of 10 using blocks
- Practice
-
-
Adding two digit numbers using blocks
- Activities: 1 course, 0 extra
-
Adding multiples of 10
- Activities: 3 course, 4 extra
-
-
- Adding multiples of 10
- Tutorial
-
-
-
- Adding multiples of 10.
- Practice
-
-
-
- Adding multiples of 10
- Tutorial
-
Extra activities
-
-
- Adding multiples of 10
- Printable
-
-
-
- Adding multiples of 10
- Tutorial
-
-
-

- Addition problem solving
- Assessment
-
-
-

- Adding lots of 10
- Practice
-
-
Adding two digit numbers by rounding then estimating
- Activities: 1 course, 2 extra
Extra activities
-
-
- Estimating
- Printable
-
-
-
- Estimating Answer sheet
- Printable
-
-
Adding multiples of 10
- Activities: 1 course, 3 extra
-
Adding two-digit numbers using the split strategy
- Activities: 5 course, 2 extra
-
Adding two-digit numbers using the jump strategy
- Activities: 6 course, 5 extra
Extra activities
-
-
- Jump Strategy/Method Explained
- Tutorial
-
-
-
- Jump Strategy/Method
- Tutorial
-
-
-

- Addition of two digit numbers
- Challenge
-
-
-

- Addition of Two Digit Numbers
- Assessment
-
-
Adding two-digit numbers using the written strategy
- Activities: 5 course, 8 extra
Extra activities
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Practice
-
-
-

- Addition of two digit numbers
- Tutorial
-
-
Adding two digit numbers
- Activities: 2 course, 1 extra
-
-
- Adding two digit numbers
- Practice
-
-
-
- Adding two digit numbers
- Practice
-
Extra activities
-
-
- Adding two digit numbers
- Printable
-
-
-
12 learning outcomes – click to view
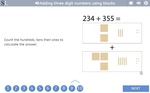
2.NBT.7 – Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
-
4 learning outcomes – click to view
Samples: Adding three digit numbers using blocks. Adding multiples of 10 using blocks.
-
Adding three digit numbers using blocks
- Activities: 1 course, 0 extra
-
Adding multiples of 10 using blocks
- Activities: 2 course, 0 extra
-
-
- Adding multiples of 10 using blocks
- Tutorial
-
-
-
- Adding multiples of 10 using blocks
- Practice
-
-
Place value - Subtract three digit numbers
- Activities: 1 course, 0 extra
-
Subtracting multiples of 10 using blocks
- Activities: 1 course, 0 extra
-
-
4 learning outcomes – click to view
2.NBT.8 – Mentally add 10 or 100 to a given number 100–900, and mentally subtract 10 or 100 from a given number 100–900.
-
3 learning outcomes – click to view
Samples: Adding 100. Subtracting 10 large numbers. Subtracting 100. Adding 100. Subtracting 10 large numbers. Subtracting 100.
-
Adding-on 100
- Activities: 1 course, 1 extra
-
Subtracting 10 from larger numbers
- Activities: 1 course, 1 extra
-
Subtracting 100 from larger numbers
- Activities: 1 course, 1 extra
-
-
3 learning outcomes – click to view
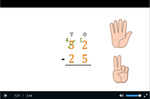
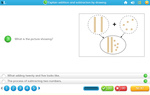
2.NBT.9 – Explain why addition and subtraction strategies work, using place value and the properties of operations. (Explanations may be supported by drawings or objects.)
-
1 learning outcomes – click to view
Samples: Explain addition and subtraction by drawing.
-
Show addition and subtraction visually
- Activities: 1 course, 0 extra
-
-
1 learning outcomes – click to view
2.MD – Measurement & Data
Mathematics
2.MD.1 – Measure the length of an object by selecting and using appropriate tools such as rulers, yardsticks, meter sticks, and measuring tapes.
-
3 learning outcomes – click to view
Samples: Units Of Measure Metric. Devices for Measuring Length. Units Of Measure Metric.
-
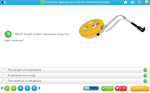
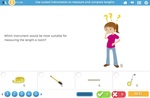
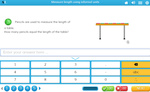
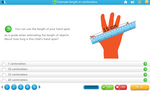
Using the appropriate tools for measuring length
- Activities: 5 course, 0 extra
-
-
- Devices for Measuring Length
- Tutorial
-
-
-
- Which measuring device
- Practice
-
-
-
- Units Of Measure Metric
- Tutorial
-
-
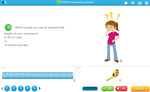
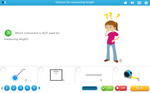
Use instruments to measure length.
- Activities: 2 course, 0 extra
-
-
- Units Of Measure Metric
- Tutorial
-
-
-
- Devices for measuring length
- Practice
-
-
3 learning outcomes – click to view
2.MD.2 – Measure the length of an object twice, using length units of different lengths for the two measurements; describe how the two measurements relate to the size of the unit chosen.
-
2 learning outcomes – click to view
Samples: Measuring Length (using informal units). Measure length using informal units. Length.
-
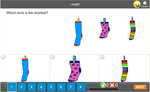
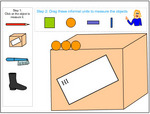
Measure length using informal units.
- Activities: 2 course, 5 extra
-
-
- Measure length using informal units
- Practice
-
Extra activities
-
-
- Length
- Practice
-
-
-

- Length
- Assessment
-
-
-

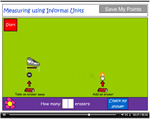
- Measuring using informal units
- Practice
-
-
-

- Using informal units to measure length.
- Whiteboard
-
-
-
2 learning outcomes – click to view
2.MD.3 – Estimate lengths using units of inches, feet, centimeters, and meters.
2.MD.4 – Measure to determine how much longer one object is than another, expressing the length difference in terms of a standard length unit.
-
1 learning outcomes – click to view
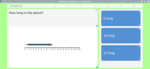
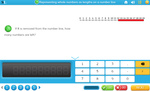
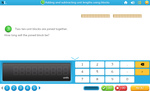
Samples: Measuring in centimeters. Measure length in centimeters. Measure length (problem solving).
-
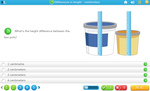
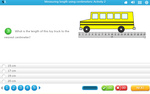
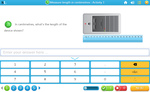
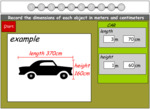
Measure length in centimeters
- Activities: 10 course, 3 extra
-
-
- Measuring in centimeters
- Tutorial
-
-
-
- Measure length in centimeters
- Practice
-
-
-
- Measure length (problem solving)
- Practice
-
-
-
- Estimate length in centimeters
- Practice
-
-
-
- Differences in length - centimeters
- Practice
-
-
-
- Measuring with a ruler (cm)
- Printable
-
-
-
- Measuring (cm)
- Printable
-
-
-
- Measuring With A Ruler
- Tutorial
-
-
-
- Units Of Measure Metric
- Tutorial
-
Extra activities
-
-
- Measuring in centimeters
- Printable
-
-
-

- Measuring Length in Centimeters
- Practice
-
-
-

- Measuring using the Centimeter
- Practice
-
-
-
1 learning outcomes – click to view
Mathematics
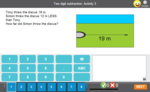
2.MD.5 – Use addition and subtraction within 100 to solve word problems involving lengths that are given in the same units, e.g., by using drawings (such as drawings of rulers) and equations with a symbol for the unknown number to represent the problem.
-
2 learning outcomes – click to view
Samples: Measuring in Centimetres. Measuring in metres. Measure length in centimeters : Activity 1. Measuring in metres.
-
Measure length in centimetres
- Activities: 1 course, 1 extra
-
-
- Measuring in Centimetres
- Tutorial
-
Extra activities
-
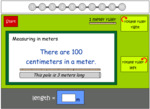
Measure length in metres
- Activities: 1 course, 4 extra
-
-
- Measuring in metres
- Tutorial
-
Extra activities
-
-
- Measuring in metres
- Printable
-
-
-

- Measuring in Meters
- Practice
-
-
-
2 learning outcomes – click to view
2.MD.6 – Represent whole numbers as lengths from 0 on a number line diagram with equally spaced points corresponding to the numbers 0, 1, 2, ..., and represent whole-number sums and differences within 100 on a number line diagram.
-
2 learning outcomes – click to view
Samples: Representing lengths on a number line. Adding and subtracting unit lengths using blocks.
-
Representing lengths on a number line
- Activities: 2 course, 0 extra
-
Adding and subtracting unit lengths
- Activities: 1 course, 0 extra
-
-
2 learning outcomes – click to view
Mathematics
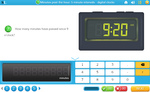
2.MD.7 – Tell and write time from analog and digital clocks to the nearest five minutes, using a.m. and p.m.
-
3 learning outcomes – click to view
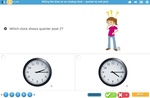
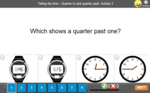
Samples: Reading digital time. Telling the time. Telling the time on an analog clock - quarter to and past.
-
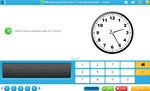
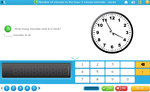
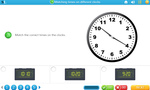
Reading time - five minute intervals
- Activities: 8 course, 2 extra
-
-
- Reading digital time
- Tutorial
-
-
-
- Counting by 5's on a clock face
- Tutorial
-
-
-
- Matching times on different clocks
- Practice
-
Extra activities
-
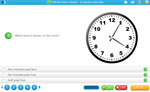
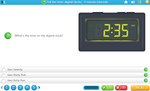
Reading Time - to the minute
- Activities: 4 course, 9 extra
-
-
- Telling the time
- Tutorial
-
-
-
- Reading Five Minute Intervals
- Tutorial
-
-
-
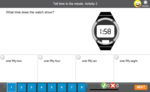
- Tell time to the minute
- Practice
-
-
-
- Reading Time - to the minute
- Practice
-
Extra activities
-
-
- Tell time to the minute: Activity 2
- Practice
-
-
-

- Telling the time
- Practice
-
-
-

- Telling the time
- Practice
-
-
-
- Reading analog to one minute intervals
- Printable
-
-
-
- Recording analog time in digital format
- Printable
-
-
-
- Time
- Printable
-
-
-

- Time
- Assessment
-
-
Telling the time on an analog clock - quarter to and past
- Activities: 2 course, 9 extra
Extra activities
-
-
3 learning outcomes – click to view
2.MD.8 – Solve word problems involving dollar bills, quarters, dimes, nickels, and pennies, using $ and ¢ symbols appropriately. Example: If you have 2 dimes and 3 pennies, how many cents do you have?
Mathematics
2.MD.9 – Generate measurement data by measuring lengths of several objects to the nearest whole unit, or by making repeated measurements of the same object. Show the measurements by making a line plot, where the horizontal scale is marked off in whole-number units.
2.MD.10 – Draw a picture graph and a bar graph (with single-unit scale) to represent a data set with up to four categories. Solve simple put-together, take-apart, and compare problems (See Glossary, Table 1. http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ ) using information presented in a bar graph.
-
4 learning outcomes – click to view
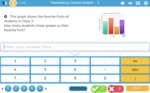
Samples: Data - picture graphs. Create a Column Graph. Data. Column graphs. Picture graphs. Data. Column graphs.
-
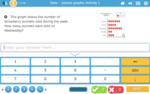
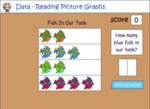
Interpret data presented using picture graphs.
- Activities: 2 course, 4 extra
-
-
- Data - picture graphs
- Practice
-
-
-
- Picture graphs.
- Practice
-
Extra activities
-
-
- Display data using picture graphs
- Printable
-
-
-
- Data - picture graphs: Activity 2
- Practice
-
-
-

- Reading picture graphs
- Practice
-
-
-

- Making picture graphs
- Practice
-
-
Data & Graphs - Column Graph Creator
- Activities: 0 course, 1 extra
Extra activities
-
-

- Create a Column Graph
- Whiteboard
-
-
Interpret data presented using simple column graphs
- Activities: 0 course, 6 extra
Extra activities
-
-

- Data
- Assessment
-
-
-

- Data
- Assessment
-
-
-

- Data Problem Solving
- Assessment
-
-
-

- Data Problem Solving
- Assessment
-
-
-

- Making a bar graph
- Practice
-
-
-

- Reading a column graph
- Practice
-
-
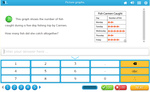
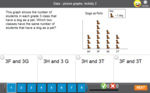
Column graphs
- Activities: 4 course, 6 extra
-
-
- Column graphs
- Tutorial
-
-
-
- Column graphs
- Practice
-
-
-
- Interpreting Column Graphs - 3
- Practice
-
-
-
- Reading column graphs
- Printable
-
Extra activities
-
-
- Display data using a simple column graph
- Printable
-
-
-
- Collecting data and making a bar graph
- Printable
-
-
-
- Data
- Printable
-
-
-
- Data
- Printable
-
-
-
- Data Problem Solving
- Printable
-
-
-
- Data Problem Solving
- Printable
-
-
-
4 learning outcomes – click to view
2.G – Geometry
Mathematics
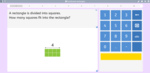
2.G.1 – Recognize and draw shapes having specified attributes, such as a given number of angles or a given number of equal faces. (Sizes are compared directly or visually, not compared by measuring.) Identify triangles, quadrilaterals, pentagons, hexagons, and cubes.
-
3 learning outcomes – click to view
Samples: Quadrilaterals. Constructing 2D shapes. Features of three-dimensional objects. Naming two-dimensional shapes.
-
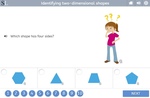
Identifying two-dimensional shapes
- Activities: 5 course, 0 extra
-
-
- Quadrilaterals
- Tutorial
-
-
-
- Naming two-dimensional shapes
- Tutorial
-
-
-
- Regular and irregular shapes
- Tutorial
-
-
-
- Identifying two-dimensional shapes
- Practice
-
-
-
- Naming two-dimensional shapes
- Tutorial
-
-
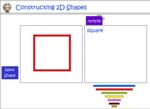
Construct and draw two dimensional shapes
- Activities: 3 course, 3 extra
-
-
- Constructing 2D shapes
- Tutorial
-
-
-
- Constructing 2D shapes
- Tutorial
-
-
-
- Drawing shapes
- Printable
-
Extra activities
-
-
- Drawing 2D shapes
- Printable
-
-
-

- Constructing 2D shapes
- Practice
-
-
-

- Draw Shapes
- Printable
-
-
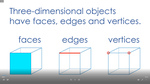
Describe the features of three-dimensional objects
- Activities: 4 course, 8 extra
-
-
- Identifying corners on 3D objects
- Tutorial
-
Extra activities
-
-

- Space 3D Problem Solving
- Assessment
-
-
-
- Space 3D Problem Solving
- Printable
-
-
-

- Space 3D Problem Solving
- Assessment
-
-
-
- Space 3D Problem Solving
- Printable
-
-
-
- Properties of 3D objects
- Printable
-
-
-

- Identifying faces on 3D objects
- Practice
-
-
-

- Identifying corners on 3D Objects
- Practice
-
-
-
3 learning outcomes – click to view
2.G.2 – Partition a rectangle into rows and columns of same-size squares and count to find the total number of them.
-
1 learning outcomes – click to view
Samples: Counting by using rows. Counting by using rows. Partitioned rectangles.
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
-
- Counting by using rows
- Tutorial
-
-
-
- Counting by using rows
- Tutorial
-
-
-
- Partitioned rectangles
- Practice
-
-
-
1 learning outcomes – click to view
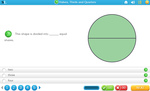
2.G.3 – Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Recognize that equal shares of identical wholes need not have the same shape.
-
5 learning outcomes – click to view
Samples: Halving groups. Introduction to Fractions. Quarters. Fractions of groups. Writing fractions. Halving groups.
-
Halving groups
- Activities: 3 course, 1 extra
-
-
- Halving groups
- Tutorial
-
-
-
- Halving groups
- Practice
-
-
-
- Halves: identifying an equal share
- Tutorial
-
Extra activities
-
-
- Halving groups
- Printable
-
-
Halves, thirds and quarters
- Activities: 2 course, 1 extra
-
-
- Introduction to Fractions
- Tutorial
-
-
-
- Halves, thirds and quarters
- Practice
-
Extra activities
-
-
- Thirds
- Printable
-
-
Halves, quarters and eighths
- Activities: 7 course, 10 extra
-
-
- Quarters
- Tutorial
-
-
-
- Eighths
- Tutorial
-
-
-
- Halves and Quarters
- Practice
-
-
-
- Halves and quarters
- Tutorial
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Quarters and eighths
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-
- Halves and quarters tutorial
- Tutorial
-
-
-
- Fraction of objects and shapes
- Practice
-
-
-

- Compare to a half tutorial
- Tutorial
-
-
-

- Compare to a half
- Practice
-
-
-

- Comparing fractions tutorial
- Tutorial
-
-
-
- Identifying halves and quarters
- Practice
-
-
-

- Comparing fractions
- Practice
-
-
Dividing groups into halves and quarters
- Activities: 5 course, 5 extra
-
-
- Fractions of groups
- Tutorial
-
-
-
- Dividing groups into fractions
- Practice
-
-
-
- Fraction- Groups
- Printable
-
Extra activities
-
-
- Fractions
- Printable
-
-
-
- Fractions Problem Solving
- Printable
-
-
-

- Fractions
- Assessment
-
-
-

- Fractions Problem Solving
- Assessment
-
-
Identifying fractions
- Activities: 6 course, 4 extra
-
-
- Writing fractions
- Tutorial
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying simple fractions
- Practice
-
-
-
- Fractions Chart
- Printable
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Representing fractions
- Printable
-
-
-
- Identifying fractions
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-

- Identifying fractions
- Practice
-
-
-
5 learning outcomes – click to view